Catalan Numbers
Author: Mihnea Brebenel
Prerequisites
| Resources | ||||
|---|---|---|---|---|
| cp-algo | Well documented article. | |||
The Catalan numbers are a sequence of positive integers that can be very useful in counting problems in combinatorics. The -th Catalan can be expressed as follows using binomial coeffiecients:
They also have the recurrence formula
which can also be expressed as
The first Catalan numbers are
| n | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 5 | 14 | 42 |
Applications
The Catalan numbers can be used to represent a wide variety of things.
For example, is equal to the number of valid parenthesis expressions of length . Take, for instance, :
()()()(())()()(())((()))(()())
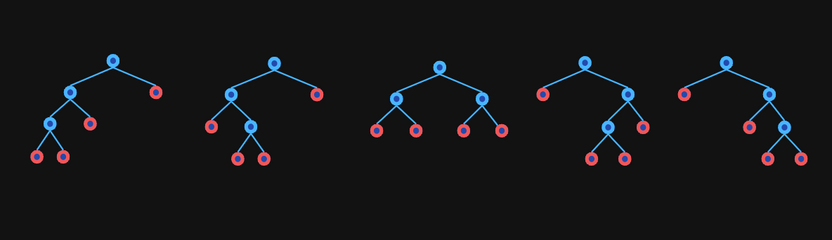
It's also equal to the number of full binary trees with leaves. The following image shows the binary trees with leaves:
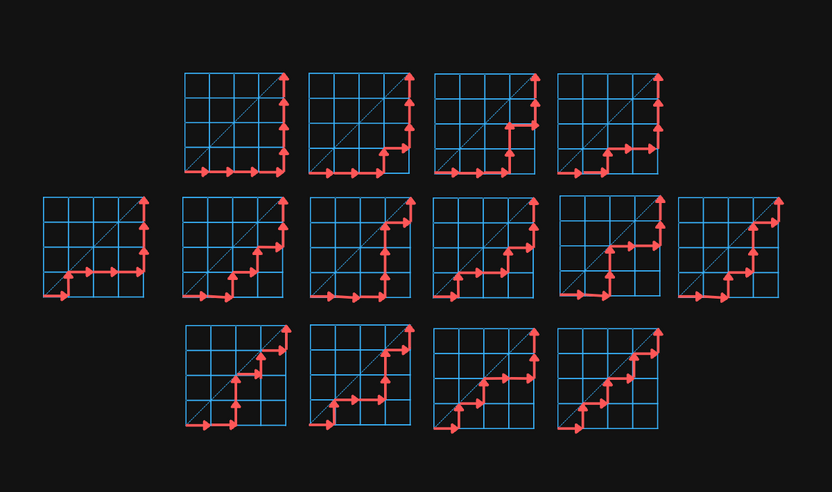
is also the number of monotonic lattice paths along the edges of a grid that don't pass above the diagonal. The paths start in the lower left corner and ends in the upper right corner.
For example, there are paths in a grid:
The next two examples are a bit more niche, but they're still interesting to think about.
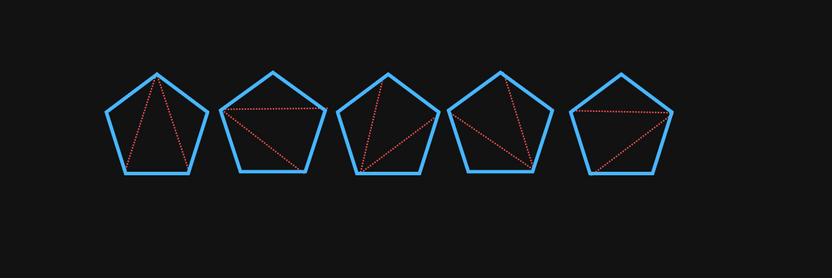
Consider a convex polygon with sides divided into triangles by connecting vertices with non-intersecting lines. The number of different ways to divide the polygon in this way is equal to .
Here's the particular case for in which we have :
is also equal to the number of mountain ranges of length consisting of upstrokes and downstrokes.
Bracket Sequences I
Focus Problem – try your best to solve this problem before continuing!
Explanation
The problem is a direct application of Catalan numbers. The answer for is the Catalan Number.
Implementation
Time Complexity:
C++
#include <iostream>using namespace std;const int MOD = 1e9 + 7;const int MAXN = 1e6;long long fac[MAXN + 1];long long inv[MAXN + 1];
Python
MAXN = 10**6MOD = 10**9 + 7fac = [0] * (MAXN + 1)inv = [0] * (MAXN + 1)Code Snippet: Combinatorics Functions (from the module) (Click to expand)n = int(input())
Problems
| Status | Source | Problem Name | Difficulty | Tags | |
|---|---|---|---|---|---|
| LC | Easy | Show TagsCatalan, Combinatorics | |||
| SPOJ | Normal | Show TagsCatalan, Combinatorics | |||
| CSES | Hard | Show TagsCatalan, Combinatorics |
Module Progress:
Join the USACO Forum!
Stuck on a problem, or don't understand a module? Join the USACO Forum and get help from other competitive programmers!